Generalidades
La
Teoría de Conjuntos se atribuye al matemático Georg Cantor (1845-1918) y
constituye el cimiento de la Matemática Moderna.
Conjunto y elemento, son considerados términos
primitivos en este contexto, es decir que no pueden ser definidos. Sólo se
puede tener una noción intuitiva de su significado:
"Un
conjunto, es cualquier colección bien definida de entes que reciben el nombre de
elementos del conjunto”.
Cabe
destacar aquí la importancia de la expresión "bien definida", ya que
diremos que un conjunto está bien definido, si y sólo si, dado un
elemento, puede determinarse si pertenece o no, al conjunto.
Por
ejemplo, las vocales del alfabeto español, constituyen un conjunto, ya
que dada cualquier letra, podemos afirmar inequívocamente si pertenece o no a
dicho conjunto. Sin embargo, si nos referimos a las letras del alfabeto,
no conforman un conjunto, ya que debe especificarse del alfabeto de qué lengua
estamos hablando, ya que letras como la ñ, por ejemplo, pertenecen al
alfabeto español y no al inglés, luego la colección no está bien definida.
Pertenecia.
Un
conjunto puede tener un número finito de elementos (como el conjunto de las
letras vocales del alfabeto español), o un número infinito de elementos (como el
conjunto de los números naturales).
En
general, se usan letras mayúsculas para denotar a los conjuntos y letras
minúsculas para designar a los elementos.
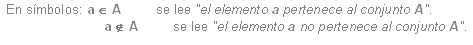
Formas de definir un conjunto.
Los
conjuntos se pueden definir por enumeración o extensión y por comprensión o
propiedades.
En
el primer caso se nombran todos los elementos del conjunto y sólo los
de él, por lo tanto esta forma de definir un conjunto es aplicable sólo a
conjuntos finitos y resulta útil para conjuntos con un número relativamente
reducido de elementos. Por ejemplo:
V = {a, e, i, o, u}
En
el segundo caso se nombra una o más propiedades de los elementos del
conjunto y sólo de ellos, por lo tanto esta forma de definir conjuntos es
aplicable aún para conjuntos infinitos. Por ejemplo:
V = {x / x es una vocal del alfabeto español}
De
esta manera, al tratarse de conjuntos bien definidos, podemos efectuar las
siguientes afirmaciones:

Igualdad de conjuntos.
Dados dos conjuntos A y B, se
dice que son iguales, y se denota por A=B, sii están formados por los
mismos elementos.
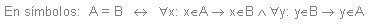
Es
decir que, estrictamente hablando, se trata de un mismo conjunto con dos nombres
distintos. Cabe destacar que en la noción de conjunto, el orden de sus
elementos, no tiene ninguna importancia en cuanto a su determinación.
Es decir que:
{a, b} = {b, a} ya que ambos miembros de la igualdad son en realidad, el
mismo conjunto.
Inclusión.
Dados dos conjuntos A y B, se dice que A está incluido en B y se denota
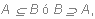 sii
todo elemento de A es elemento de B.
sii
todo elemento de A es elemento de B.
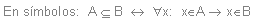
Dados dos conjuntos A y B, se dice que A está estrictamente incluido en B,
o bien A es subconjunto propio de B y se denota
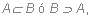 si todo
elemento de A es también elemento de B, pero existe al menos un elemento
en B que no es elemento de A.
si todo
elemento de A es también elemento de B, pero existe al menos un elemento
en B que no es elemento de A.
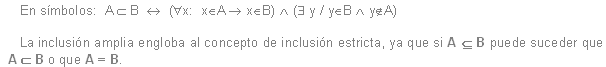
Propiedades de la inclusión.
·
Propiedad Reflexiva: Todo conjunto es subconjunto de
sí mismo.
·
Propiedad Transitiva: Si un conjunto es subconjunto
de otro y éste subconjunto de un tercero, entonces el primero es subconjunto
del tercero.
·
Propiedad Antisimétrica: Si un conjunto es
subconjunto de otro y éste subconjunto del primero, entonces los conjuntos son
iguales.
·
Vacío siempre presente: El conjunto vacío está
incluído en todo conjunto.
Conjuntos
especiales.
Se
extiende el concepto de conjunto definiendo el conjunto vacío
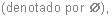 como aquel que no contiene
elemento alguno y conjunto unitario, a aquel que tiene un
solo elemento.
como aquel que no contiene
elemento alguno y conjunto unitario, a aquel que tiene un
solo elemento.
Otro caso de conjunto especial es el conjunto referencial o universal,
que se denota con "U", y al cual pertenecen todos los elementos a
los que se hace referencia en el estudio. En los ejemplos anteriores, el
conjunto universal es el conjunto de todas las letras.
Por
último, otro conjunto especial cuya aplicación es importante, es el denominado
conjunto potencia de un conjunto A, denotado por P(A),
que tiene por elementos a todos los posibles subconjuntos de A.
