|
MAQUINA DE MEALY
Ejercicio
1:
Dada la siguiente Máquina de Mealy,
realizar:
a-
la definición formal
b-
el grafo
correspondiente
c-
tomando como estado
inicial q0, las salidas para las siguientes
entradas:
x1=
{aabc}
x2= {bac}
x3= {acc}
d- idem, pero tomando como estado inicial q1.
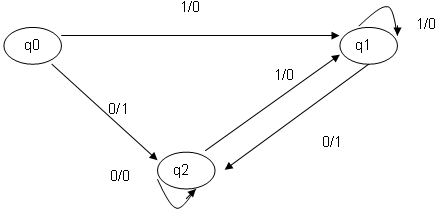
Ejercicio 2:
Dada la Máquina de Mealy representada en el
siguiente grafo, se pide:
a)
Escribir las tablas “f”
y “g” correspondientes al grafo
b)
Encontrar las cadenas
de salida que corresponden a las siguientes cadenas
de entrada, tomando como estado inicial q1:
x1=
{1100} x2=
{1010} x3= {11110000}
c)
Definir la máquina
mínima equivalente.
d)
Idem al punto b, pero
con la máquina minimizada.
ME =
[ { 0, 1} , { 0, 1} , {q0, q1, q2 }, f , g ]
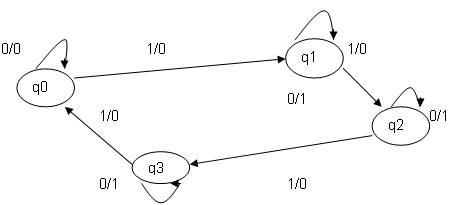
Ejercicio 3:
Dada la Máquina de Mealy del grafo que se muestra a
continuación, se pide:
a)
Escribir las tablas “f”
y “g” correspondientes al grafo
b)
Encontrar la cadena de
salida que corresponde a la siguiente cadena de
entrada, tomando como estado inicial q1 y q3:
x1 =
{110110} x2 ={01110111}
c)
Definir la máquina
mínima equivalente
d)
Idem al punto b, pero
obteniéndola de la máquina minimizada.
ME =
[ { 0,1} , {0,1} , { q0, q1, q2, q3 } , f , g ]
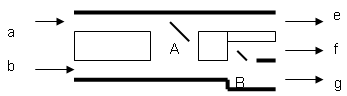
Ejercicio 4:
Diseñar un a Máquina de Mealy que represente el
comportamiento del dispositivo distribuidor que se
muestra. Las válvulas A y B cambian de posición
luego de desviar un objeto, luego nótese que B
cambia siempre mientras que A lo hace según su
entrada. La posición “\”
por “1”, luego las posiciones indicadas en la figura
para A-B son 1-1. Se pide: definir formalmente la
máquina detallando sus componentes y representar el
grafo correspondiente.
AUTÓMATA FINITO
Ejercicio 1:
Diseñar un autómata finito que acepte un número
IMPAR de 1 (unos).
(
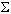= {1}).
Ejercicio
2:
Diseñar un autómata finito que acepte un número PAR
de 1 (unos).
(
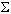= {1}).
Ejercicio
3:
Diseñar un autómata finito que acepte un número
IMPAR de 1 (unos).
(
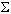= { 0,1} ).
Ejercicio
4:
Diseñar un autómata finito que acepte un número PAR
de 1 (unos).
(
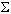= { 0, 1} ).
Ejercicio
5:
Diseñar un autómata finito que acepte una cadena
formada por 4 bits, debiendo ser:
I-
el primer elemento
igual al último
II-
el segundo elemento
igual al tercero
III-
los dos primeros
iguales a los dos últimos
Ejercicio 6:
Construir un autómata finito que NO acepte aquellas
cadenas que contengan las subtiras: ¨aa¨ o ¨bb¨. Las
tiras no tienen una longitud fija. El alfabeto al
que pertenecen es
=
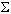{a, b}.
Ejercicio 7:
Determinar el A.F. que reconozca cada uno de los
siguientes lenguajes, que se han definido en forma
algebraica:
L1 (G) =
{0i
1 0j / i ³
1, j ³
1}
L2 (G) =
{(01)i
12j / i ³
1, j ³
1}
Ejercicio 8:
Construir un A.F. que acepte como cadenas válida:
-
solo aquellas que
comienzan con un solo 0 o un solo 1
-
si comienzan con un
solo 0, luego deben seguirle solo un número impar de
1, la cadena puede finalizar con estas condiciones o
además con un solo 0. (ej: 01110)
-
si comienzan con un
solo 1, luego deben seguirle solo un número par de
0, la cadena puede finalizar con estas condiciones o
además con un solo 1. (ej: 10001)
-
acepta la cadena 0 y la
cadena 1
Se
pide:
a)
el grafo
correspondiente
b)
la definición formal
del A.F.
MINIMIZACIÓN DE AUTÓMATA FINITO
Ejercicio
1:
Comprobar si los siguientes AFD son
equivalentes:
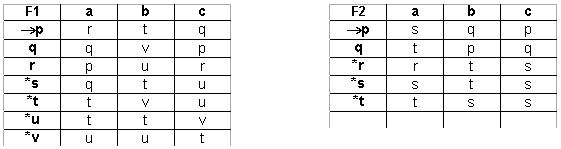
Ejercicio 2:
Determinar cuáles
de los siguientes autómatas son equivalentes entre
sí:
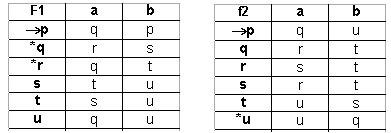
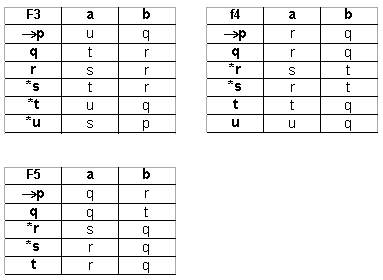
ELIMINACIÓN DE
LAMBDA
Ejercicio
1:
Ejercicio
2:
Ejercicio
3:
AUTÓMATA A PILA
Ejercicio
1:
Crear
una A.P. por cada items y verifique si se encuentran
balanceados, es decir, por cada símbolo de abertura
debe haber uno de cierre. Las entradas son:
a)
( ( ) )
b)
( ( ) )
( ( ( ) ) )
c)
[
( ) ( ( ) )
]
Ejercicio
2:
Diseñar
un A.P. (por cada items), que verifique si en un
byte leído:
a)
los
cuatro primeros bits tienen la misma cantidad de 1
que los cuatro últimos.
b)
Los
cuatro primeros bits tienen la misma cantidad de 0
que 1 los cuatro últimos
c)
Los
cuatro primeros bits constituyen la imagen refleja
de los cuatro últimos.
d)
Los
cuatro últimos bits constituyen la imagen refleja
negada de los cuatro primeros.
Ejercicio
3:
Diseñar
un A.P. que verifique si dos nibles leídos,
separados por un * (asterisco) el primero tiene la
misma cantidad de 1 que el segundo.
|
