Las expresiones regulares, son una forma distinta de representar a los Lenguajes Regulares, brindando una notación concisa de los mismos. Observemos que según lo expresado anteriormente estamos tratando lenguajes y no cadenas de caracteres, por lo tanto una expresión regular única denotará  un conjunto de cadenas que definirá el Lenguaje.

Los lenguajes regulares, al igual que las expresiones regulares, resultan muy interesantes desde el punto de vista práctico porque se utilizan para la especificación en la construcción de los analizadores léxicos  (Analizar un texto y extraer las componentes lexicográficas- “tokens” )

Definición de expresiones regulares 

Para un alfabeto dado 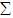 , sólo serán Expresiones Regulares aquellas que se obtienen aplicando un número finito un cierto conjunto de reglas.

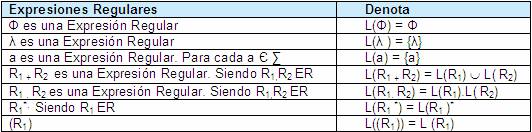
 Las Expresiones Regulares sobre un Lenguaje 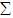, son interesantes desde el punto de vista teórico porque constituyen el menor conjunto de lenguajes sobre 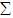, que es cerrado con respecto a las propiedades de concatenación, la cerradura de Klene, además que en su definición da contención al Lenguaje Vacío 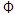, la cadena vacía , y los lenguajes unitarios para cada símbolo del alfabeto.  

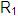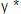Es importante notar () permite la utilización de paréntesis para agrupar, aunque ya existe un orden de precedencia en donde: la cerradura tienen precedencia sobre la concatenación y la esta última tiene precedencia sobre la unión. Haciendo uso de  los operadores de unión, concatenación  , es posible expresar lenguajes mas extensos.

Ejemplos

1) Dar una expresión regular que permita describir  un Lenguaje L1 para las patentes en la República Argentina. Es sabido que estas se componen de tres letras, seguidas de tres números.

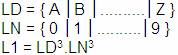
2) Dar una expresión regular que permita representar todos los nombres de calles de una determinada región.